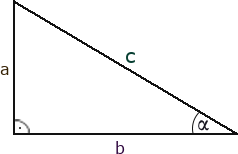
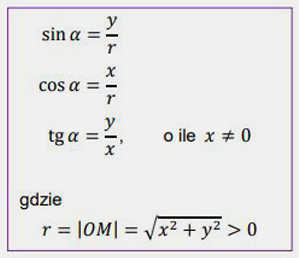Sinus, cosinus, tangens kąta ostrego
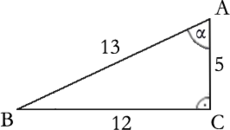
Odp. A.
$$\sin\alpha = \frac{\raisebox{.01in}{\scriptsize{dł. dalszej przyprostokątnej}}}{\raisebox{-.01in}{\scriptsize{dł. przeciwprostokątnej}}} = \dfrac{12}{13}$$
Przykład
Niech $\cos\alpha=\dfrac{2}{5}$, gdzie $\alpha$ jest kątem ostrym. Oblicz sinus kąta $\alpha$.
Rozwiązanie
Skorzystamy z jedynki trygonometrycznej:
$$\sin^2\alpha+\cos^2\alpha=1$$
$$\sin^2\alpha=1-\cos^2\alpha$$
Teraz za $\cos\alpha$ podstawimy $\dfrac{2}{5}$.
$$\sin^2\alpha=1-\left(\dfrac{2}{5}\right)^2$$
$$\sin^2\alpha=1-\dfrac{4}{25}$$
$$\sin^2\alpha=\dfrac{25}{25}-\dfrac{4}{25}$$
$$\sin^2\alpha=\dfrac{21}{25}$$
To równanie ma dwa rozwiązania.
(Nie wiesz czemu? Wyjaśnienie w Szkole Kwadratowej.)
$$\sin\alpha=\sqrt{\dfrac{21}{25}} \quad \vee \quad \sin\alpha=\text{-}\sqrt{\dfrac{21}{25}}$$
Ponieważ sinus kąta ostrego jest dodatni, a $\alpha$ jest kątem ostrym, więc ujemne rozwiązanie odrzucamy.
Ostatecznie:
$$\sin\alpha=\sqrt{\dfrac{21}{25}}=\dfrac{\sqrt{21}}{5}$$
Odp. B.
Skorzystamy z jedynki trygonometrycznej:
$$\sin^2\alpha+\cos^2\alpha=1$$
$$\cos^2\alpha=1-\sin^2\alpha$$
Teraz za $\sin\alpha$ podstawimy $\dfrac{1}{2}$.
$$\cos^2\alpha=1-\left(\dfrac{1}{2}\right)^2$$
$$\cos^2\alpha=1-\dfrac{1}{4}$$
$$\cos^2\alpha=\dfrac{4}{4}-\dfrac{1}{4}$$
$$\cos^2\alpha=\dfrac{3}{4}$$
To równanie ma dwa rozwiązania.
(Nie wiesz czemu? Wyjaśnienie w Szkole Kwadratowej.)
$$\cos\alpha=\sqrt{\dfrac{3}{4}} \quad \vee \quad \cos\alpha=\text{-}\sqrt{\dfrac{3}{4}}$$
Ponieważ cosinus kąta ostrego jest dodatni, a $\alpha$ jest kątem ostrym, więc ujemne rozwiązanie odrzucamy.
Ostatecznie:
$$\cos\alpha=\sqrt{\dfrac{3}{4}}=\dfrac{\sqrt{3}}{2}$$
Odp. B.
Zauważamy, że dla $\cos\alpha=0{,}8$ spełniona jest jedynka trygonometryczna:
$$0{,}6^2 + 0{,}8^2 = 0{,}36 + 0{,}64 = 1$$
Korzystamy ze wzoru na tangens:
$$\tg\alpha=\frac{\sin\alpha}{\cos\alpha} \hspace{0.8cm}$$
$$\tg\alpha=\frac{0{,}6}{0{,}8}=0{,}75$$
Odp. C.
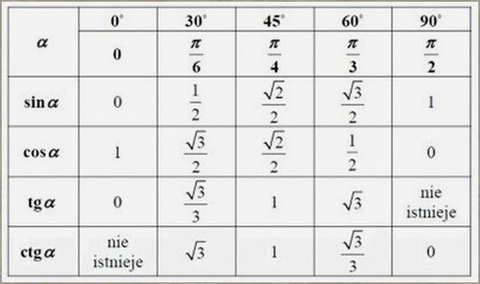
Miarę kąta $\alpha$ odczytujemy wprost z tabelki wartości funkcji trygonometrycznych.
Odp. C.
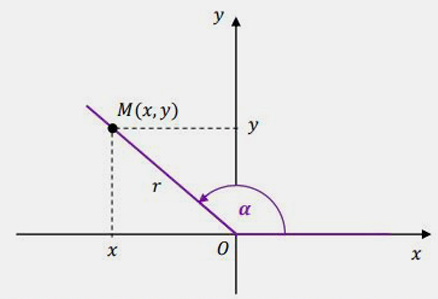
Korzystamy ze wzoru na tangens dowolnego kąta:
$$\tg \alpha = \dfrac{y}{x}=\dfrac{2}{\text{-}6}=\text{-}\dfrac{1}{3}$$