Funkcje trygonometryczne dowolnego kąta

Do tej pory rozważaliśmy funkcje trygonometryczne kąta ostrego, czyli z przedziału $(0^\circ,90^\circ)$.
Nic nie stoi nam jednak na przeszkodzie, by wyliczyć je także dla kątów spoza tego przedziału.
Tu rozstajemy się z trójkątem prostokątnym - nie będzie nam już potrzebny.
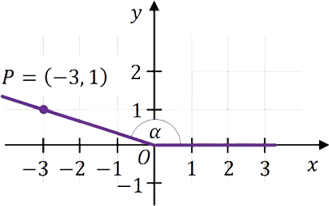
Weźmiemy za to nasz kąt $\alpha$ i zaczepimy jego wierzchołek w początku układu współrzędnych, czyli w punkcie $(0,0)$. Ważne by jedno ramię kąta $\alpha$ pokryło się z dodatnią półosią $Ox$, tak jak na rysunku. Takie położenie kąta $\alpha$ nazwiemy standardowym.
Na ramieniu odchodzącym kąta $\alpha$ oznaczymy punkt $M(x,y)$. Punkt ten może leżeć bliżej wierzchołka lub dalej - wedle uznania. Nie ma to znaczenia. Ważne, byśmy znali jego współrzędne. Dzięki temu wyliczymy długość promienia wodzącego $r$ oraz wartości funkcji trygonometrycznych kąta $\alpha$.

Przykład 1.
Niech kąt $\beta$ leży w układzie współrzędnych w położeniu standardowym. Końcowe ramię niech przechodzi przez punkt $P(-4,3)$. Oblicz wartości wszystkich funkcji trygonometrycznych kąta $\beta$.
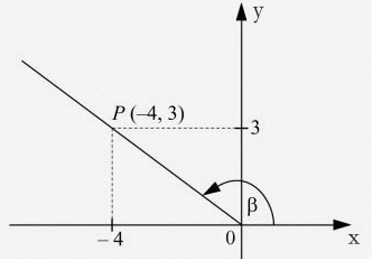
Wyliczymy $\sin\alpha$, $\cos\alpha$ i $\tg\alpha$.
By wyliczyć $\sin\alpha$, potrzebujemy znać długość promienia wodzącego $r=|OP|$.
$r>0$
$$\hspace{1cm} r=\sqrt{(-4)^2+3^2}$$
$$\hspace{1cm} r=\sqrt{25}$$
$$\hspace{1cm} r=5$$
Ponadto, ponieważ punkt $P=(-4,3)$, więc $x=-4$ oraz $y=3$.
Wyliczymy wartości funkcji trygonometrycznych.
$$\hspace{1cm} \sin\alpha=\frac{y}{r}=\dfrac{3}{5}$$
$$\hspace{1cm} \cos\alpha=\frac{x}{r}=\dfrac{-4}{5}=-\dfrac{4}{5}$$
$$\hspace{1cm} \tg\alpha=\frac{y}{x}=\dfrac{-3}{4}=-\dfrac{3}{4}$$
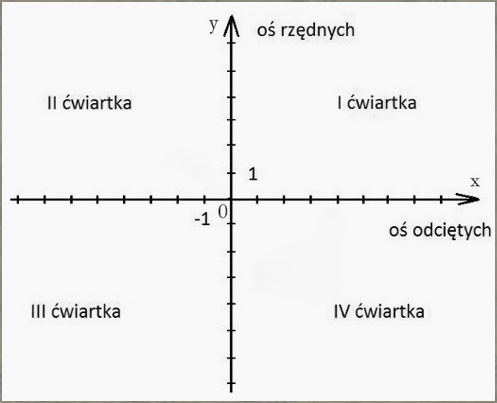
Ćwiartki
Powiemy, że kąt $\beta$ z powyższego przykładu znajduje się w II ćwiartce.
Chodzi o ćwiartki układu współrzędnych wyznaczone przez oś $Ox$, czyli oś odciętych, oraz oś $Oy$, czyli oś rzędnych.
Kąty ostre, czyli o mierze z przedziału $(0^\circ,90^\circ)$ są w I ćwiartce.
Kąty rozwarte, czyli o mierze z przedziału $(90^\circ,180^\circ)$ są w II ćwiartce.
Kąt miary $15^\circ$ jest w $I$ ćwiartce.
$210^\circ$ to $III$ ćwiartka.
Kąt $120^\circ$ znajduje się w $II$ ćwiartce.