Trygonometria

Przydadzą nam się trójkąty, odcinki i kąty.
Czy wiesz już, że tangens to nie żadna tropikalna choroba zakaźna?
Przeniesiemy się do Starożytnego Egiptu... Chwyćcie czasozmieniacz... 🌟
Nie kojarzę tego grobowca... ale sami spójrzcie!
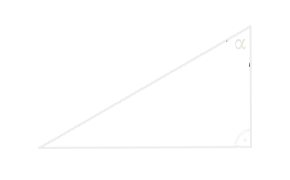
Widzicie trójkąt prostokątny?
Niech jego wierzchołki to $A, B, C$, boki zaś $a, b, c$.
Kąt przy wierzchołku $A$ natomiast znaczyć będzie grecka litera α (alfa).

Czyli sinus, cosinus, tangens i cotangens kąta ostrego
To po prostu stosunki długości boków w trójkącie prostokątnym.
Powiemy, że sinus, cosinus, tangens i cotangens to funkcje trygonometryczne.
Przykład 1.
Oblicz wartość sinusa, cosinusa i tangensa kąta $\alpha$.
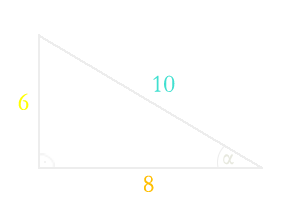
Pamiętasz? W trójkącie prostokątnym mamy dwie przyprostokątne i przeciwprostokątną.
Dalsza przyprostokątna (z punktu widzenia wierzchołka kąta $\alpha$) ma długość $\textcolor{yellow}{6}$.
Bliższa ma długość $\textcolor{orange}{8}$.
Przeciwprostokątna ma długość $\textcolor{aqua}{10}$.
$\sin\alpha = \frac{\raisebox{.04in}{\scriptsize{dł. dalszej przyprostokątnej}}}{\raisebox{-.04in}{\scriptsize{dł. przeciwprostokątnej}}} = \dfrac{\textcolor{yellow}{6}}{\textcolor{aqua}{10}} = \dfrac{3}{5}$
$\tg\alpha = \frac{\raisebox{.04in}{\scriptsize{dł. dalszej przyprostokątnej}}}{\raisebox{-.04in}{\scriptsize{dł. bliższej przyprostokątnej}}} = \dfrac{\textcolor{yellow}{6}}{\textcolor{orange}{8}} = \dfrac{3}{4}$
$\cos\alpha = \frac{\raisebox{.04in}{\scriptsize{dł. bliższej przyprostokątnej}}}{\raisebox{-.04in}{\scriptsize{dł. przeciwprostokątnej}}} = \dfrac{\textcolor{orange}{8}}{\textcolor{aqua}{10}} = \dfrac{4}{5}$
Jak widać, najważniejsze to:
1. Zlokalizować odpowiedni kąt.
2. Odczytać długości dalszej i bliższej przyprostokątnej oraz długość przeciwprostokątnej.
3. Użyć zaklęć sinusa, cosinusa i tangensa.✨



Czas wrócić do Twierdzy... 🌟 O, profesor Pitagoras!

Przykład 2.
Oblicz cosinus kąta $\beta$ trójkąta ABC (rys.).
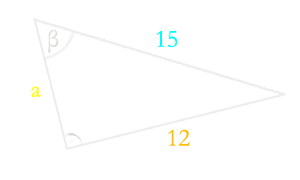
Cosinus, jak już wiecie, to stosunek długości bliższej przyprostokątnej do długości przeciwprostokątnej, czyli
$$\cos\beta=\frac{\textcolor{yellow}{a}}{\textcolor{aqua}{15}}$$
Jak jednak wyliczyć $a$?
Oczywiście korzystając z zależności, którą kiedyś zauważyłem. Kiedyś, to znaczy w czasach starożytnych. 😎
$$a^2+12^2=15^2$$
$$a^2+144=225$$
$$a^2=81, a>0$$
$$a=9$$
Zatem
$$\cos\beta=\frac{9}{15}=\frac{3}{5}$$