Zadania z geometrii analitycznej





Punkt $C=(0,0)$ jest wierzchołkiem trójkąta prostokątnego $ABC$, którego wierzchołek $A$ leży na osi $Ox$, a wierzchołek $B$ na osi $Oy$ układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka $C$ przecina przeciwprostokątną $AB$ w punkcie $D=(3,4)$.
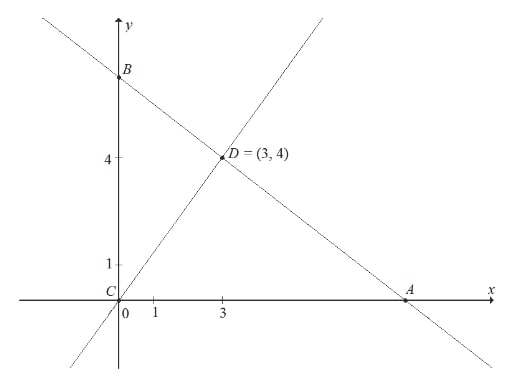
Współrzędne punktów $A$ i $B$ to
$$A(x_A,0)$$
$$B(0,y_B)$$
Długość odcinka $AB$ to
$$|AB|=\sqrt{x_A^2+y_B^2}$$
By znaleźć $x_A$ i $y_B$, wyznaczymy równanie prostej $y_{AB}=ax+b$ przechodzącej przez te punkty.
Ponieważ prosta $y_{CD}$ zawiera wysokość trójkąta $ABC$, więc proste $y_{AB}$ i $y_{CD}$ są prostopadłe.
Dla ich współczynników kierunkowych zachodzi więc
$$a_{AB} \cdot a_{CD} = -1$$
Mamy, że
$$a_{CD} = \dfrac{4-0}{3-0}=\dfrac{4}{3}$$
$$a_{AB} \cdot \dfrac{4}{3} = -1$$
$$a_{AB} = -\dfrac{3}{4}$$
Ponadto, by wyznaczyć wyraz wolny $b$ prostej $y_{AB}=-\dfrac{3}{4}x+b$ , skorzystamy z faktu, że przechodzi ona przez punkt $D=(\textcolor{6e6f14}{4,3})$.
$$\textcolor{6e6f14}{4} = -\dfrac{3}{4} \cdot \textcolor{6e6f14}{3} + b$$
$$4 = -\dfrac{9}{4} + b$$
$$b = 4 + \dfrac{9}{4} = \dfrac{25}{4}$$
Równanie prostej $y_{AB}$ to zatem
$$y_{AB}=-\dfrac{3}{4}x+\dfrac{25}{4}$$
Ponieważ przechodzi ona przez punkty $A(\textcolor{2a5f5f}{x_A,0})$ i $B(\textcolor{571e68}{0,y_B})$, więc
$$\textcolor{2a5f5f}{0}=-\dfrac{3}{4}\textcolor{2a5f5f}{x_A}+\dfrac{25}{4}$$
$$-\dfrac{25}{4}=-\dfrac{3}{4}\textcolor{2a5f5f}{x_A}$$
$$\textcolor{2a5f5f}{x_A}=\dfrac{25}{3}$$
oraz
$$\textcolor{571e68}{y_B}=-\dfrac{3}{4} \cdot \textcolor{571e68}{0} + \dfrac{25}{4}$$
$$\textcolor{571e68}{y_B}=\dfrac{25}{4}$$
Zatem
$$|AB|=\sqrt{\textcolor{2a5f5f}{x_A}^2+\textcolor{571e68}{y_B}^2}=\sqrt{\left(\dfrac{25}{3}\right)^2+\left(\dfrac{25}{4}\right)^2}$$
$$|AB|=\sqrt{\dfrac{25^2}{3^2}+\dfrac{25^2}{4^2}}=\sqrt{25^2 \left( \dfrac{1}{3^2}+\dfrac{1}{4^2} \right)}$$
$$|AB|=25\sqrt{\left( \dfrac{1}{9}+\dfrac{1}{16} \right)}=25\sqrt{\dfrac{16+9}{9 \cdot 16}}$$
$$|AB|=25\sqrt{\dfrac{25}{144}}=25 \cdot \dfrac{5}{12}=\dfrac{125}{12}$$