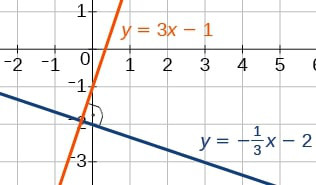Równanie prostej

Bez układu współrzędnych się nie obejdzie. Wszystkie figury, odcinki, proste czy punkty, jakie się tu pojawią, będziemy nań umieszczać.
Niech elficka prezycja będzie waszym drogowskazem. 🏹
Postać kierunkowa prostej
$\textcolor{ffffe6}{y =} \textcolor{d2f6e1}{a}\textcolor{ffffe6}{x +} \textcolor{f7e0c3}{b}$
$\textcolor{d2f6e1}{a}$ - współczynnik kierunkowy
$\textcolor{f7e0c3}{b}$ - wyraz wolny
Postać ogólna prostej
$\textcolor{#ffffe6}{Ax + By + C = 0}$

Przykład 1.
Sprawdź, czy punkt $(1,4)$ należy do prostej o równaniu $y=3x+1$.
$$4=3 \cdot 1 +1$$
$$4=4$$
Odpowiedź: Tak.

Proste równoległe
Proste równoległe to na przykład: $$\textcolor{b5dcff}{y = \dfrac{1}{2}x+5}$$
$$\textcolor{ffd4b3}{y = \dfrac{1}{2}x+2}$$ Współczynniki kierunkowe obu prostych są równe $\dfrac{1}{2}$.
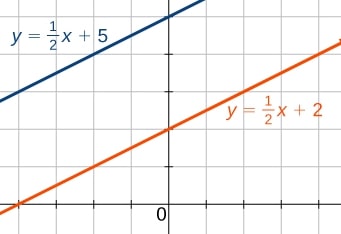
Proste prostopadłe
Proste są prostopadłe, gdy iloczyn ich współczynników kierunkowych jest równy $\text{-}1$.
Proste prostopadłe to na przykład: $$\textcolor{b5dcff}{y = -\dfrac{1}{3}x-2}$$
$$\textcolor{ffd4b3}{y = 3x-1}$$
Iloczyn współczynników kierunkowych obu prostych jest równy $$\textcolor{b5dcff}{-\dfrac{1}{3}} \cdot \textcolor{ffd4b3}{3} = -1$$