Punkt i odcinek w układzie współrzędnych

Bez układu współrzędnych się nie obejdzie. Wszystkie figury, odcinki, proste czy punkty, jakie się tu pojawią, będziemy nań umieszczać.
Niech elficka prezycja będzie waszym drogowskazem. 🏹
Punkt w układzie współrzędnych
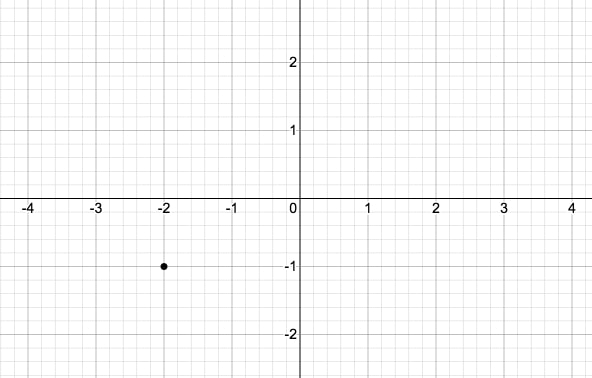
W układzie współrzędnych zaznaczono punkt $(-2,-1)$.

Odcinek w układzie współrzędnych
Odcinek, czyli ograniczony kawałek prostej.
Długość odcinka o końcach w punktach $\textcolor{ffffe6}{A(x_A,y_A)}$ i $\textcolor{ffffe6}{B(x_B,y_B)}$ wyraża się zaklęciem $$\textcolor{ffffe6}{|AB|=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2}}$$
Zaklęcie to jest przy okazji tym na odległość między dwoma punktami $A$ i $B$.
Przykład 1.
Oblicz długość odcinka o końcach w punktach $A(-1,5)$ i $B(3,2)$.
Mamy, że
$$|AB|=\sqrt{(-1-3)^2+(5-2)^2}$$
$$|AB|=\sqrt{16+9}=\sqrt{25}=5$$

Środek $\textcolor{ffffe6}{S}$ odcinka o końcach w punktach $\textcolor{ffffe6}{A(x_A,y_A)}$ i $\textcolor{ffffe6}{B(x_B,y_B)}$ ma współrzędne $$\textcolor{ffffe6}{S=\left(\dfrac{x_A+x_B}{2},\dfrac{y_A+y_B}{2}\right)}$$
Przykład 1.
Wyznacz współrzędne środka odcinka o końcach w punktach $A(-1,4)$ i $B(5,2)$.
Mamy, że
$$S=\left(\dfrac{-1+5}{2},\dfrac{4+2}{2}\right)$$
$$S=(2,3) \hspace{1.9cm}$$