Wektory

Bez układu współrzędnych się nie obejdzie. Wszystkie figury, odcinki, proste czy punkty, jakie się tu pojawią, będziemy nań umieszczać.
Niech elficka prezycja będzie waszym drogowskazem. 🏹
Wektor to odcinek, który ma zwrot i kierunek
Oto przykłady wektorów:
$$\textcolor{#d8fff2}{\vec{u}=[3,4]} \hspace{2cm} \textcolor{#f1ffd8}{\vec{v}=[-1,0]} \hspace{2cm} \textcolor{#daffd9}{\vec{w}=[5,-10]}$$
Zwrot wektora to określenie, gdzie ma początek, a gdzie koniec - strzałkę.
Kierunek wektora to kierunek prostej, na którek leży.
Długość wektora
Zaklęcie długości wektora $\textcolor{#d8fff2}{\vec{u}=[x,y]}$ to $$\textcolor{#d8fff2}{|\vec{u}|=\sqrt{x^2+y^2}}$$
Przykład 1.
Oblicz długość wektora $\vec{u}=[4,-3]$.
Mamy, że
$$|\vec{u}|=\sqrt{4^2+(-3)^2}$$
$$|\vec{u}|=\sqrt{16+9}=\sqrt{25}=5$$


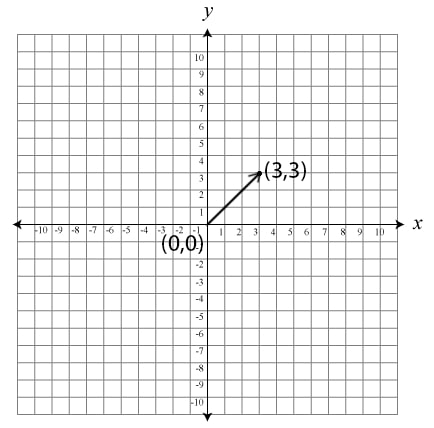
Wektor, którego początek znajduje się w konkretnym punkcie układu współrzędnych to wektor zaczepiony.
Wyczarowałam wektor $\textcolor{ddfef3}{\vec{u} = [3,3]}$ zaczepiony w początku układu współrzędnych, czyli w punkcie $(0,0)$.
Wektor $\textcolor{ddfef3}{\vec{u}}$ to zatem wektor zaczepiony.
Współrzędne wektora o początku w punkcie $(0,0)$ i końcu w $(3,3)$ wyznaczymy odejmując współrzędne punktu końcowego od początkowego:
$$\textcolor{e1ece9}{\vec{u}=[3-0,3-0]=[3,3]}$$


Dodawanie i odejmowanie wektorów
Wektory dodajemy i odejmujemy po współrzędnych.
Weźmy dwa wektory:
$$\textcolor{#d8fff2}{\vec{u}=[3,4]} \hspace{2cm} \textcolor{#f1ffd8}{\vec{v}=[-1,0]}$$
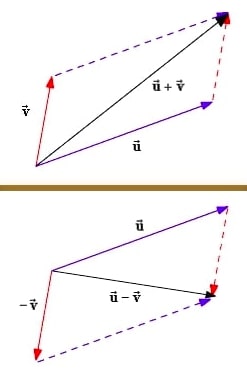
Wówczas suma wektorów to
$$\textcolor{#d8fff2}{\vec{u}} + \textcolor{#f1ffd8}{\vec{v}} = \textcolor{#d8fff2}{[3,4]} + \textcolor{#f1ffd8}{[-1,0]}=[\textcolor{#d8fff2}{3}+\textcolor{#f1ffd8}{(-1)},\textcolor{#d8fff2}{4}+\textcolor{#f1ffd8}{0}]=[2,4]$$
Różnica wektorów to
$$\textcolor{#d8fff2}{\vec{u}} - \textcolor{#f1ffd8}{\vec{v}} = \textcolor{#d8fff2}{[3,4]} - \textcolor{#f1ffd8}{[-1,0]}=[\textcolor{#d8fff2}{3}-\textcolor{#f1ffd8}{(-1)},\textcolor{#d8fff2}{4}-\textcolor{#f1ffd8}{0}]=[4,4]$$

Dane są wektory $\vec{AB}=[0,3]$ i $\vec{AC}=[-4,5]$. Wyznacz wektor $\vec{AB}+\vec{AC}$.
$$\vec{AB}+\vec{AC}=[0,8]+[-4,10]=[0+(-4),8+10]=[-4,18]$$