Równanie okręgu

Bez układu współrzędnych się nie obejdzie. Wszystkie figury, odcinki, proste czy punkty, jakie się tu pojawią, będziemy nań umieszczać.
Niech elficka prezycja będzie waszym drogowskazem. 🏹
Równanie okręgu
Weźmy jakiś punkt $\textcolor{#ffffe6}{(a,b)}$ na płaszczyźnie, gdzie $\textcolor{#ffffe6}{a}$ oraz $\textcolor{#ffffe6}{b}$ to pewne liczby rzeczywiste. Wówczas
równanie okręgu ma postać:
$$\textcolor{#ffffe6}{(x-a)^2+(y-b)^2=r^2}$$
gdzie $\textcolor{#ffffe6}{r}$ jest promieniem okręgu. Punkt $\textcolor{#ffffe6}{(a,b)}$ jest jego środkiem.
Na przykład
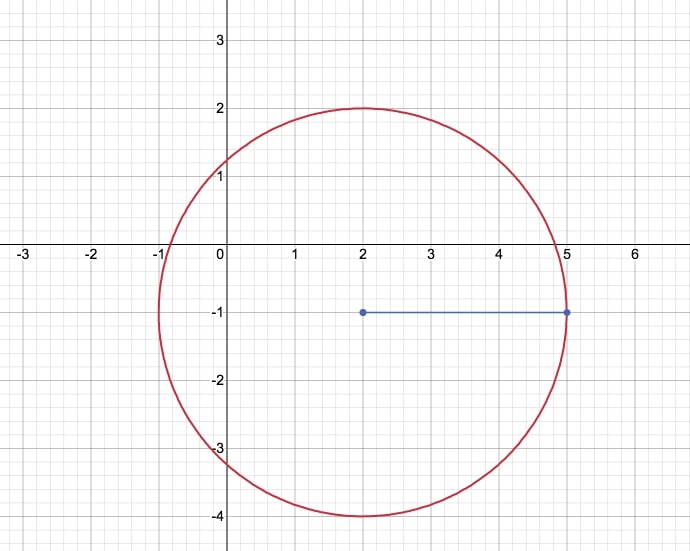
$$\textcolor{#C5FEE7}{(x-2)^2+(y+1)^2=9}$$
jest równaniem okręgu o środku w punkcie $\textcolor{#C5FEE7}{(2,-1)}$ i promieniu $\textcolor{#C5FEE7}{r=3}$.