Matura podstawowa z matematyki grudzień 2023
180 minut 46 punktów
Odp. C.
Korzystamy z praw działań na potęgach.
$$\left(3^{-2,4} \cdot 3^{^{\normalsize{\frac{2}{5}}}}\right)^{\normalsize{\frac{1}{2}}} = 3^{^{\normalsize{{-\frac{24}{10} \cdot \frac{1}{2}}}}} \cdot 3^{^{\normalsize{\frac{2}{5} \cdot \frac{1}{2}}}} = 3^{^{\normalsize{-\frac{6}{5}}}} \cdot 3^{^{\normalsize{\frac{1}{5}}}} = 3^{^{\normalsize{-\frac{6}{5} + \frac{1}{5}}}} = 3^{^{\normalsize{-\frac{5}{5}}}} = 3^{^{\normalsize{-1}}}=\dfrac{1}{3}$$
Odp. D.
Korzystamy ze wzoru na różnicę logarytmów o takich samych podstawach:
$$\log_a b - \log_a c = \log_a {\dfrac{b}{c}} \hspace{1.1cm}$$
$$\hspace{1cm} \log_2 96 - \log_2 3 = \log_2 \frac{96}{3} = \log_2 32 = 5$$
Odp. B.
Bank dolicza odsetki od kwoty bieżacego kapitału, więc korzystamy ze wzoru na procent składany:
$$K=K_0(1+r)^n$$
gdzie $K$ - kapitał końcowy, $K_0$ - kapitał początkowy, $r$ - roczna stopa oprocentowania, $n$ - ilość okresów kapitalizacji
$$K_0=\dfrac{K}{(1+r)^n} \hspace{0.5cm}$$
$$\hspace{1.4cm} K_0=\dfrac{4851}{(1+0{,}05)^2}=4400\text{ zł}$$

Odp. A.
Korzystamy z interpretacji geometrycznej wartości bezwzględnej (odległości na osi liczbowej).
$|x-a| < b$ oznacza, że odległość $x$ od $a$ jest mniejsza od $b$
$|x-2| < 5$ oznacza, że odległość $x$ od $2$ jest mniejsza od $5$
$$x \in (-3,7)$$
Wykaż, że dla każdej liczby całkowitej nieparzystej $n$ liczba $3n^2+4n+1$ jest podzielna przez $4$.
Korzystamy z wiedzy o dowodzeniu podzielności.
Założenie:
$n = 2k + 1, k \in \mathbb{Z}$
Teza:
$3n^2+4n+1 = 4l, l \in \mathbb{Z}$
Dowód:
$L_T=3n^2+4n+1 = 3(2k + 1)^2+4(2k + 1)+1 = 3(4k^2+4k+1)+8k+5=12k^2+20k+8=4(\underbrace{3k^2+5k+2}_{\normalsize{\in \mathbb{Z}}})\text{ =}P_T$
$\hspace{16.8cm} \text{c.n.d.}$
Odp. C.
Korzystamy z wiedzy o układach równań liniowych.
Dany w zadaniu układ rozwiążemy metodą przeciwnych współczynników. Mnożymy pierwsze równanie przez $-2$, otrzymując poniższy układ:
$$\begin{cases} -2x +6y -10 = 0 \\ \hspace{0.6cm} 2x + y + 3 = 0 \end{cases}$$
$$\hspace{1.4cm} 7y-7=0$$
$$\hspace{2.1cm} 7y=7$$
$$\hspace{2.2cm} y=1$$
Uwaga: Rozwiązaniem układu równań jest para liczb $(x,y)$, ale tylko w odpowiedzi C. mamy $y=1$, więc nie musimy już wyliczać $x$.
Odp. C.
Korzystamy z wiedzy o skracaniu wyrażeń wymiernych.
$$\dfrac{x+3}{x^2+4x+4} \cdot \dfrac{x^2+2x}{2x+6} = \dfrac{\cancel{x+3}}{(x+2)\cancel{(x+2)}} \cdot \dfrac{x\cancel{(x+2)}}{2\cancel{(x+3)}}=\dfrac{x}{2x+4}$$
Odp. D.
Korzystamy z wiedzy o rozkładzie wielomianu.
Pierwiastkiem wielomianu $W$ jest $-1$, czyli $W(-1)=0$.
$$0=-3(-1)^2-(-1)^2+k(-1)+1$$
$$0=-3-1-k+1 \hspace{2.2cm}$$
$$k=3 \hspace{4.3cm}$$
Rozwiąż równanie $$\bm{2x^3+3x^2=10x+15}$$ Zapisz obliczenia.
Odp. Rozwiązaniami równania są liczby: $(-\sqrt{5}),(-\dfrac{3}{2}),\sqrt{5}$.
Rozwiązujemy dane w zadaniu równanie wielomianowe metodą grupowania.
$$\hspace{0.8cm} 2x^3+3x^2-10x-15=0$$
$$\hspace{0.6cm} x^2(2x+3)-5(2x+3)=0$$
$$\hspace{1.6cm} (2x+3)(x^2-5)=0$$
$$2(x+\dfrac{3}{2})(x-\sqrt{5})(x+\sqrt{5})=0$$
$$x+\dfrac{3}{2}=0 \quad \text{lub} \quad x-\sqrt{5}=0 \quad \text{lub} \quad x+\sqrt{5}=0$$
$$x=-\dfrac{3}{2} \quad \text{lub} \quad x=\sqrt{5} \quad \text{lub} \quad x=-\sqrt{5}$$
$$x \in \{-\sqrt{5},-\dfrac{3}{2},\sqrt{5}\}$$
Funkcja liniowa $f$ jest określona wzorem $f(x)=-\dfrac{1}{6}x+\dfrac{2}{3}$ .
Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F - jeśli jest fałszywe.

Odp. PF
Znajdujemy miejsce zerowe funkcji $f$:
$$0=-\dfrac{1}{6}x+\dfrac{2}{3}$$
$$\dfrac{1}{6}x=\dfrac{2}{3} \hspace{1.5cm}$$
$$x=4 \hspace{1.3cm}$$
Funkcja dla argumentu $x=0$ przyjmuje wartość
$$f(0)=-\dfrac{1}{6}\cdot0+\dfrac{2}{3}=\dfrac{2}{3}$$
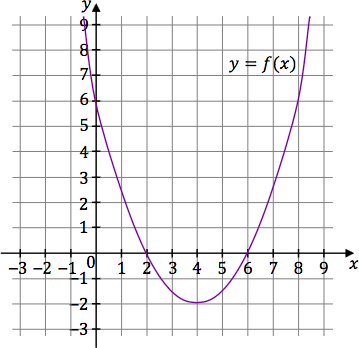
W kartezjańskim układzie współrzędnych $(x,y)$ przedstawiono fragment wykresu funkcji kwadratowej $f$ (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji $f$, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
Odp. D.
Zbiór wartości funkcji $f$ odczytujemy z wykresu.
Najmniejsza wartość funkcji $f$ to wartość w wierzchołku paraboli równa $y = \text{-}2$. Ramiona paraboli są skierowane do góry, więc każde $y$ większa od $\text{-}2$ również jest wartością funkcji $f$.
Zapisz poniżej w postaci przedziału zbiór wszystkich argumentów, dla których funkcja $f$ przyjmuje wartości ujemne.
.................................................................................................................................................
Odp. $(2,6)$
Wartości ujemnych funkcji $f$ szukamy na wykresie tam, gdzie parabola leży poniżej osi $Ox$. Wartości ujemne funkcja $f$ przyjmuje dla $x \in (2,6)$.
Uzupełnij zdanie. Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A–F i wpisz te litery w wykropkowanych miejscach.
Wzór funkcji $f$ można przedstawić w postaci: ………. oraz ………. .
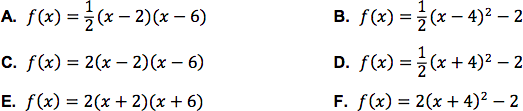
Odp. A. oraz B.
Korzystamy z wiedzy o postaci iloczynowej i postaci kanonicznej funkcji kwadratowej.
Z wykresu odczytujemy pierwiastki funkcji $f$: są to $x_1=2$ i $x_2=-4$.
$$f(x)=a(x-2)(x+4)$$
Z wykresu odczytujemy współrzędne wierzchołka paraboli: $(4,-2)$.
$$f(x)=a(x-4)^2-2 \hspace{0.4cm}$$
Współczynnik $a$ wyliczamy z równania $f(0)=6$ (punkt $(0,6)$ należy do wykresu funkcji $f$).
$$6=a(0-4)^2-2$$
$$8=16a \hspace{1.5cm}$$
$$a=\dfrac{1}{2} \hspace{1.8cm}$$
Funkcja kwadratowa $g$ jest określona za pomocą funkcji $f$ (zobacz rysunek na stronie 11) następująco: $g(x)=f(x+1)$. Na jednym z rysunków A–D przedstawiono, w kartezjańskim układzie współrzędnych $(x,y)$, fragment wykresu funkcji $y=g(x)$.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Fragment wykresu funkcji $y=g(x)$ przedstawiono na rysunku
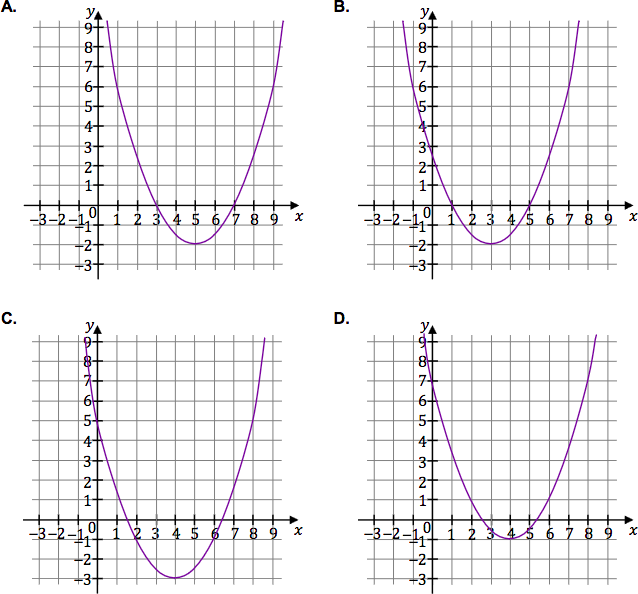
Odp. B.
Korzystamy z wiedzy o przekształcaniu wykresu funkcji.
Dodanie liczby $1$ do argumentu funkcji przesuwa wykres funkcji o jeden w lewo.
Uwaga: Każdy punkt funkcji $f$ przesuwamy o jeden w lewo, więc wystarczy skupić się na jednym, np. na wierzchołku paraboli. Jeśli wcześniej wierzchołek miał współrzędne $(4,-2)$, to po przesunięciu ma współrzędne $(3,-2)$.
Odp. D.
Korzystamy z wiedzy o funkcji wykładniczej.
Obliczamy wartość funkcji $T$ dla $x=20$:
$$T(20) = 78 \cdot 2^{−0,05\cdot20} + 22 = 78 \cdot 2^{−1} + 22 =61\text{ }^{\circ}\text{C}$$
Odp. A.
Korzystamy z wiedzy o ciągu arytmetycznym.
$$a_6=a_3+3r \hspace{0.2cm}$$
Obliczamy różnicę ciągu $(a_n)$:
$$a_2+r=a_3 \hspace{1.5cm}$$
$$r=a_3-a_2$$
$$\hspace{0.3cm} r=9-4=5$$
Obliczamy szósty wyraz ciągu $(a_n)$:
$$ a_6=9+3\cdot5=24$$
Ciąg $(a_n)$ jest określony dla każdej liczby naturalnej $n \ge 1$. Suma $n$ początkowych wyrazów tego ciągu jest określona wzorem $S_n=4 \cdot (2n-1)$ dla każdej liczby naturalnej $n \ge 1$.
Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.

Odp. PF
Korzystamy z wiedzy o ciągach liczbowych.
$$a_1=S_1=4 \cdot (2^1-1)=4 \hspace{0.8cm}$$
$$\hspace{0.3cm} a_2=S_2-S_1=4 \cdot (2^2-1) - 4 = 8$$
Odp. A.
Korzystamy z własności trzech kolejnych wyrazów ciągu geometrycznego.
$$(1-2a)\cdot48=12^2 \hspace{0.6cm}$$
$$1-2a=3$$
$$\hspace{1.1cm} a=-1$$
Dane są dwa kąty o miarach $\alpha$ oraz $\beta$, spełniające warunki:
$\alpha \in (0^\circ,180^\circ)$ i $\tg\alpha = -\dfrac{2}{3}$ oraz $\beta \in (0^\circ,180^\circ)$ i $\cos\beta = \dfrac{1}{\sqrt{10}}$.
Na rysunkach A-F w kartezjańskim układzie współrzędnych $(x,y)$ zaznaczono różne kąty - w tym kąt o mierze $\alpha$ oraz kąt o mierze $\beta$. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią $Ox$, a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: $A$ lub $B$, lub $C$, lub $D$, lub $E$, lub $F$.
Uzupełnij tabelę. Wpisz w każdą pustą komórkę tabeli właściwą odpowiedź, wybraną spośród oznaczonych literami A-F.
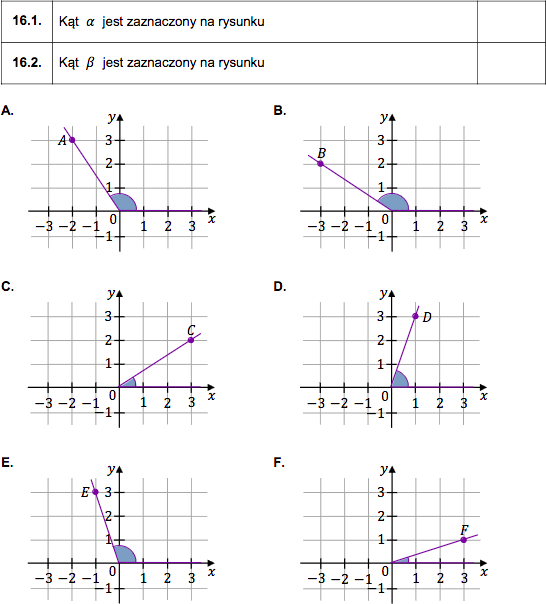
Odp. 16.1. B. oraz 16.2. D.
Korzystamy ze wzorów na funkcje trygonometryczne dowolnego kąta.
Jeśli ramię kąta $\alpha$ przecina punkt o współrzędnych $(x,y)$ oraz $r = \sqrt{x^2+y^2}$, to
w podpunkcie B. :
$$\tg\alpha=\dfrac{y}{x}=\dfrac{2}{-3}=-\dfrac{2}{3} \hspace{1.1cm}$$
w podpunkcie D. :
$$\cos\alpha=\dfrac{x}{r}=\dfrac{1}{\sqrt{1^2+3^2}}=\dfrac{1}{\sqrt{10}} \hspace{0.5cm}$$
Odp. C.
Korzystamy z jedynki trygonometrycznej i wzoru na tangens: $\sin^2\alpha+\cos^2\alpha=1$ oraz $\tg\alpha=\dfrac{\sin\alpha}{\cos\alpha}$.
$$\cos^2\alpha=1-\sin^2\alpha \hspace{1.4cm}$$
$$\cos^2\alpha=1-\left(\dfrac{\sqrt{5}}{3}\right)^2 \hspace{1.1cm}$$
$$\hspace{2.5cm} \cos^2\alpha=1-\dfrac{5}{9}=\dfrac{4}{9}\text{, } \alpha\text{ - ostry, więc} \cos\alpha>0$$
$$\cos\alpha=\dfrac{2}{3} \hspace{2.5cm}$$
$$\tg\alpha=\dfrac{\dfrac{\sqrt{5}}{3}}{\dfrac{2}{3}}=\dfrac{\sqrt{5}}{\cancel{3}} \cdot \dfrac{\cancel{3}}{2}=\dfrac{\sqrt{5}}{2}$$
Odp. D.
Korzystamy z równania kierunkowego prostej i warunku na prostopadłość prostych.
Proste są prostopadłe, gdy iloczyn ich współczynników kierunkowych jest równy $-1$.
Z równania $\dfrac{3}{2} \cdot a_k = -1$ wyliczamy $a_k=-\dfrac{2}{3}$.
$$k{:}\hspace{0.2cm}y=-\dfrac{2}{3}x+b \hspace{1.2cm}$$
Prosta $k$ przechodzi przez punkt $(6,0)$:
$$0=-\dfrac{2}{3}\cdot6+b \hspace{0.5cm}$$
$$0=-4+b \hspace{1cm}$$
$$b=4 \hspace{1.8cm}$$
Odp. B.
Korzystamy z równania kierunkowego prostej i warunku na równoległość prostych.
Proste są równoległe, gdy ich współczynniki kierunkowe są równe.
$$-\dfrac{1}{2}=2m-1$$
$$\dfrac{1}{2}=2m \hspace{0.3cm}$$
$$m=\dfrac{1}{4} \hspace{0.5cm}$$
Odp. A.
Korzystamy z równania okręgu.
Okrąg jest styczny do osi $Ox$, więc długość promienia okręgu jest równa $r=2$.
$$(x-4)^2+(y-(-2))^2=2^2$$
$$\hspace{0.4cm} (x-4)^2+(y+2)^2=4$$
Odp. D.
Korzystamy ze wzoru na odległość między punktami i ze wzoru na pole trójkąta równobocznego.
$$|KL|=\sqrt{(-1-(-7))^2+(4-(-2))^2}=\sqrt{6^2+6^2}=\sqrt{72}$$
$|KL|=a$ jest długością boku trójkąta równobocznego $KLM$.
$$P=\dfrac{a^2\sqrt{3}}{4} \hspace{1.3cm}$$
$$P=\dfrac{72\sqrt{3}}{4}=18\sqrt{3}$$
Odp. B.
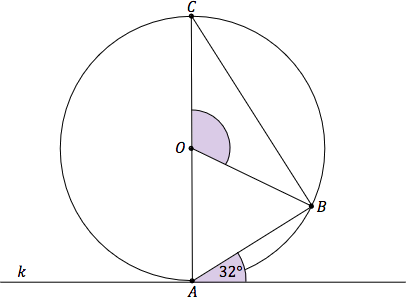
Korzystamy z wiedzy o kącie wpisanym i środkowym.
$$k \perp AC$$
$$|\angle BAC|=90^\circ-32^\circ=58^\circ$$
$\angle BAC$ jest kątem wpisanym, $\angle BOC$ jest kątem środkowym - oba oparte na tym samym łuku wyznaczonym przez cięciwę $BC$.
$$|\angle BOC| = 2 \cdot 58^\circ = 116^\circ$$
Odp. C.
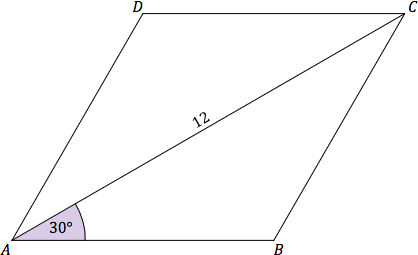
Korzystamy z wiedzy o kątach i przekątnych w rombie oraz o funkcjach trygonometrycznych.
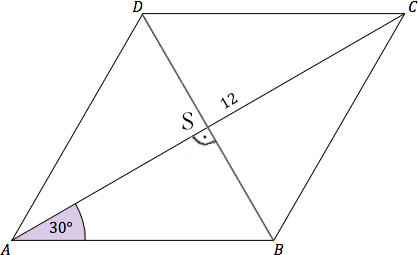
Szukane: $P$ - pole rombu $ABCD$ $$P=\dfrac{|AC| \cdot |BD|}{2}$$ Przekątne rombu przecinają się pod kątem prostym. Punkt przecięcia oznaczamy S. $$\tg30^\circ = \dfrac{|BS|}{|AS|}=\dfrac{\sqrt{3}}{3}$$ Przekątne rombu dzielą się na połowy, więc $|AS| = \dfrac{1}{2} \cdot 12 = 6$. $$\dfrac{|BS|}{6}=\dfrac{\sqrt{3}}{3} \hspace{0.2cm}$$ $$|BS|=2\sqrt{3}$$ $$|BD|=4\sqrt{3}$$ $$P=\dfrac{12 \cdot 4\sqrt{3}}{2}=24\sqrt{3}$$
Dany jest okrąg $\mathcal{O}$ o środku w punkcie $S$. Średnica $AB$ tego okręgu przecina cięciwę $CD$ w punkcie $P$ (zobacz rysunek). Ponadto: $|PB| = 4$, $|PC| = 8$ oraz $|PD| = 5$.
Oblicz promień okręgu $\mathcal{O}$. Zapisz obliczenia.
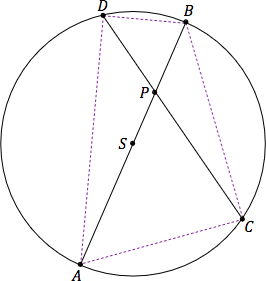
Odp. $r=7$.
Korzystamy z wiedzy o kącie środkowym i wpisanym oraz o trójkątach podobnych.
$$|\angle ABD|=|\angle ACD| \text{, kąty wpisane oparte na tym samym łuku } AD$$
$$|\angle BAC|=|\angle BDC|\text{, kąty wpisane oparte na tym samym łuku } BC$$
$$|\angle APC|=|\angle BPD| \text{, kąty wierzchołkowe } \hspace{3.7cm}$$
Trójkąty $ACP$ i $BPD$ są podobne na podstawie cechy $KKK$ (kąt-kąt-kąt).
$$\dfrac{|PA|}{|PD|}=\dfrac{|PC|}{|PB|}$$
$$\dfrac{|PA|}{5}=\dfrac{8}{4} \hspace{0.5cm}$$
$$|PA|=10 \hspace{0.3cm}$$
$$|AB|=|AP|+|PB|=10+4=14$$
Promień $r$ okręgu $\mathcal{O}$ jest równy
$$r = \dfrac{1}{2}|AB| = \dfrac{1}{2} \cdot 14 = 7$$
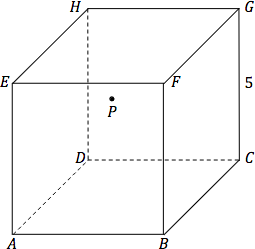
Odp. A.
Korzystamy z wiedzy o sześcianie i pojęcia kąta między prostą a płaszczyzną.
Suma odległości punktu $P$ od dwóch przeciwległych ścian równa jest długości jednej krawędzi. Są trzy pary przeciwległych ścian, więc suma odległości punktu $P$ od wszystkich ścian sześcianu jest równa $3 \cdot 5 = 15$.
Objętość ostrosłupa prawidłowego czworokątnego jest równa $384$. Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze $\alpha$ taki, że $\tg\alpha=\dfrac{4}{3}$ (zobacz rysunek).
Oblicz wysokość ściany bocznej tego ostrosłupa. Zapisz obliczenia.

Odp. $h_2 = 10$.
Korzystamy ze wzoru na objętość ostrosłupa i ze wzoru na tangens kąta ostrego.
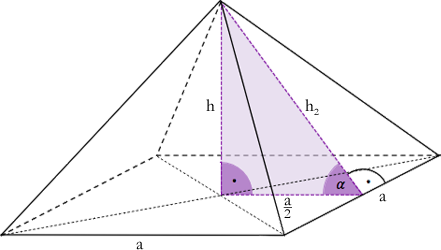
Szukane: $h_2$ - wysokość ściany bocznej ostrosłupa, $h_2 > 0$
Podstawą ostrosłupa prawidłowego czworokątnego jest kwadrat. Bok kwadratu oznaczamy $a$.
$$P=\dfrac{1}{3}a^2h = 384$$
$$\tg\alpha=\dfrac{\,h\,}{\dfrac{a}{2}}=\dfrac{4}{3} \hspace{0.3cm}$$
$$\hspace{0.9cm} 3h=4\dfrac{a}{2}$$
$$\hspace{1cm} h=\dfrac{2}{3}a$$
$$\hspace{1cm} a=\dfrac{3}{2}h$$
Wyliczamy $h$ i $a$:
$$\dfrac{1}{3} \cdot \dfrac{9h^2}{4}h = 384 \hspace{1cm}$$
$$h^3 = 512$$
$$h = 8 \hspace{0.2cm}$$
$$a = 12$$
Wyliczamy $h_2$ z twierdzenia Pitagorasa:
$$h_2^2 = h^2 + \left(\dfrac{a}{2}\right)^2$$
$$\hspace{0.5cm} h_2^2 = 64 + 36 = 100$$
$$h_2 = 10$$
E-dowód ma zapisany na pierwszej stronie specjalny sześciocyfrowy numer CAN, który zabezpiecza go przed odczytaniem danych przez osoby nieuprawnione.
Oblicz, ile jest wszystkich sześciocyfrowych numerów CAN o różnych cyfrach, spełniających warunek: trzy pierwsze cyfry są kolejnymi wyrazami ciągu arytmetycznego o różnicy $(-3)$. Zapisz obliczenia.
Możliwe pierwsze trzy cyfry numeru to: $963$, $852$, $741$ lub $630$ ($4$ możliwości).
Na pozostałych trzech miejscach możemy umieścić $7 \cdot 6 \cdot 5 = 210$ różnych cyfr, bo trzy z dziesięciu już wykorzystaliśmy.
Korzystamy z reguły mnożenia.
Wszystkich numerów jest $4 \cdot 210 = 840$.
Odp. D.
A - zdarzenie polegające na tym, że iloczyn liczb wyrzuconych oczek jest liczbą nieparzystą.
Korzystamy ze wzoru na prawdopodobieństwo zajścia zdarzenia:
$$P(A)=\dfrac{|A|}{|\Omega|}$$
$${|\Omega|}=6^2=36$$
Iloczyn dwóch liczb jest liczbą nieparzystą pod warunkiem, że obie liczby - czynniki - są nieparzyste. Zdarzenia sprzyjające to takie,
w których w obu rzutach wyrzucamy $1$, $3$ lub $5$ oczek.
$$|A| = 3 \cdot 3 = 9 = 27$$
$$P(A)=\dfrac{9}{36}=\dfrac{1}{4}$$
W hurtowni owoców wyselekcjonowane jabłko spełnia normę jakości, gdy jego masa (po zaokrągleniu do pełnych dekagramów) mieści się w przedziale [$19$ dag, $21$ dag]. Pobrano próbę kontrolną liczącą $50$ jabłek i następnie zważono każde z nich. Na poniższym wykresie słupkowym przedstawiono rozkład masy jabłek w badanej próbie. Na osi poziomej podano - wyrażoną w dekagramach - masę jabłka (w zaokrągleniu do pełnych dekagramów), a na osi pionowej przedstawiono liczbę jabłek o określonej masie.
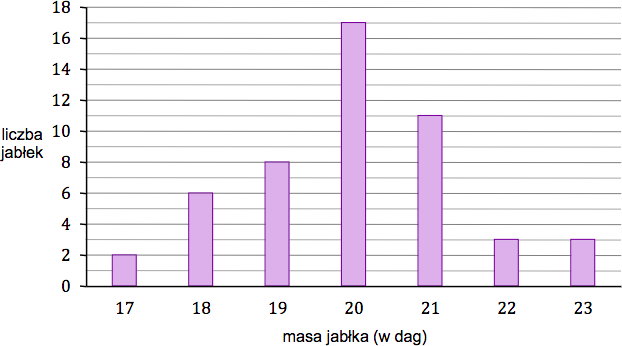
Odp. C.
A - zdarzenie polegające na tym, że wylosowane jabłko spełnia normę.
Korzystamy ze wzoru na prawdopodobieństwo zajścia zdarzenia:
$$P(A)=\dfrac{|A|}{|\Omega|}$$
$$|A| = 8 + 17 + 11 = 36 \hspace{0.4cm}$$
$$\hspace{0.6cm} |\Omega| = 2 + 6 + 36 + 3 + 3 = 50$$
$$P(A) = \dfrac{36}{50} = \dfrac{18}{25}$$
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1., 2. albo 3.
Dominanta masy $50$ zważonych jabłek (w zaokrągleniu do pełnych dekagramów) z pobranej próby kontrolnej jest równa

Odp. A. 3.
Korzystamy z wiedzy o dominancie.
Zgodnie z założeniem architekta okno na poddaszu ma mieć kształt trapezu równoramiennego, który nie jest równoległobokiem. Dłuższa podstawa trapezu ma mieć długość $12$ dm, a suma długości krótszej podstawy i wysokości tego trapezu ma być równa $18$ dm.
Oblicz, jaką długość powinna mieć krótsza podstawa tego trapezu, tak aby pole powierzchni okna było największe. Oblicz to pole. Zapisz obliczenia.
Pole trapezu wyraża się wzorem:
$$\dfrac{(a+b)h}{2}$$
Pole okna w kształcie trapezu:
$$P=\dfrac{(12 + 18 -h)}{2}h=\dfrac{h(30-h)}{2}$$
Funkcja pola zmiennej $h$:
$$P(h)=\dfrac{h(30-h)}{2}$$
Wyznaczamy dziedzinę funkcji P. Pole jest dodatnie:
$$D=(0,30)$$
Pole jest największe dla $h=15 \text{ dm}$.
Długość krótszej podstawy jest wtedy równa: $18-15=3 \text{ dm}$
