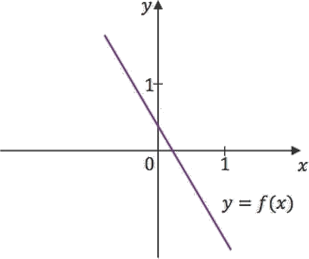
Funkcja liniowa

Funkcja liniowa to podstawowa funkcja.
Wykresem funkcji liniowej jest prosta
Funkcja to odwozorowanie.
Przykładowe funkcje liniowe:
$$\textcolor{cafff0}{f(x) = 2x} \hspace{1.5cm} \textcolor{e0f7ce}{g(x) = -3x+5} \hspace{1.5cm} \textcolor{caffd6}{h(x) = 6}$$
Dziedziną funkcji liniowej zawsze jest zbiór liczb rzeczywistych.
By znaleźć wykres funkcji liniowej, wystarczy narysować dwa punkty z jej wykresu
i poprowadzić przez nie prostą.
$\textcolor{c6da94}{a}$ - współczynnik kierunkowy decydujący o nachyleniu prostej
$\textcolor{27B9BC}{b}$ - wyraz wolny, decydujący o położeniu prostej, a dokładniej $\textcolor{36CACD}{b}$ jest miejscem przecięcią prostej z osią pionową $Oy$
Wykres funkcji liniowej
$$\textcolor{cafff0}{f(x) = 2x}$$
$\textcolor{cafff0}{f(}0\textcolor{cafff0}{) = 2 \cdot }0 = 0$, co daje punkt $(0,0)$
$\textcolor{cafff0}{f(}1\textcolor{cafff0}{) = 2 \cdot }1 = 2$, co daje punkt $(1,2)$
Narusyjemy oba punkty i poprowadzimy przez nie prostą.
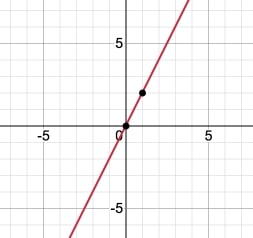
Narysowaliśmy wykres funkcji liniowej $\textcolor{cafff0}{f}$.

Miejsce zerowe funkcji liniowej
Czyli taki argument $x$, dla którego funkcja przyjmuje wartość $0$.
Miejsce zerowe znajdziemy przyrównując wzór funkcji do $0$.
Przykład 1.
Znajdź miejsce zerowe funkcji $f$ o wzorze
$f(x) = 2x+1$ .
Przyrównamy wzór funkcji do $0$.
$$2x + 1 = 0$$
$$2x = -1$$
$$x = -\dfrac{1}{2}$$
Miejsce zerowe funkcji $f$ to $x_0=-\dfrac{1}{2}$.
Przykład 2.
Znajdź miejsce zerowe funkcji $f$ o wzorze $f(x) = -3x+5$ .
$$-3x+5=0$$
$$-3x = -5$$
$$x = \dfrac{5}{3}$$
Miejsce zerowe funkcji $f$ to $x_0=\dfrac{5}{3}$.

Monotoniczność funkcji liniowej
Funkcja jest rosnąca, gdy $\textcolor{cafff0}{a > 0}$
Malejąca, gdy $\textcolor{e0f7ce}{a < 0}$
Stała, gdy $\textcolor{caffd6}{a = 0}$
i wówczas wzór funkcji
$f$ ma postać $f(x)=0 \cdot x + b = b$.
Funkcję postaci $f(x)=c$ nazywamy funkcją stałą.
Dla wszystkich argumentów przyjmuje jedną i tę samą wartość $c$.
Funkcje stałe to na przykład $f(x) = 1$ lub $h(x) = -5$.
Funcja stała
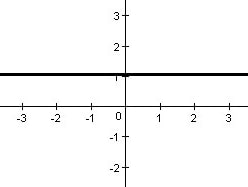
Narysowaliśmy wykres funkcji stałej $\textcolor{caffd6}{f(x) = 1}$.
Funcja rosnąca
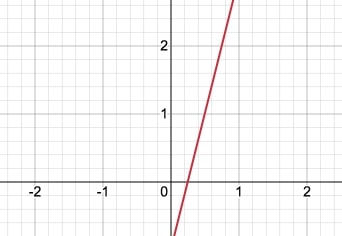
Narysowaliśmy wykres funkcji rosnącej $\textcolor{cafff0}{g(x) = 4x-1}$.
Funcja malejąca
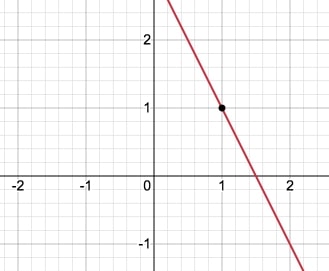
Narysowaliśmy wykres funkcji malejącej $\textcolor{e0f7ce}{h(x) = -2x+3}$.

Przykład 3.
Znajdź wzór funkcji liniowej $f$, której wykres przechodzi przez punkty $A=(-1,2)$ i $B=(3,5)$ .
Funkcja liniowa wyraża się wzorem
$$f(x)=ax+b$$
Pozostaje znaleźć $a$ i $b$.
Ponieważ mamy dwie zmiennie, więc potrzebujemy ułożyć dwa równania.
Skoro punkt $A=(-1,2)$ należy do wykresu funkcji $f$, to
$$2=a\cdot(-1)+b$$
Ponadto, jeśli punkt $B=(3,10)$ należy do wykresu funkcji $f$, to
$$5=a\cdot3+b$$
Rozwiążemy układ równań:
$$\begin{cases} -a + b = 2 \\ 3a + b = 10\end{cases}$$
Z pierwszego równania mamy, że $b=2+a$. Podstawimy za $b$ w drugim równaniu.
$$3a + 2 + a = 10$$
$$4a = 8$$
$$a = 2, \quad b = 2 + 2 = 4$$
$$f(x) = 2x + 4$$


Funkcja liniowa $f$ przyjmuje wartość $2$ dla argumentu $0$, a ponadto $f(4)-f(2)=6$. Wyznacz wzór funkcji $f$.
Oblicz wartość współczynnika $a$.
Skoro funkcja $f$ jest liniowa, to ma wzór
$$f(x)=ax+b$$
Szukane: $a$ - współczynnik kierunkowy
Skoro $f(\textcolor{1a7862}{0})=\textcolor{1a7862}{2}$, to
$$\textcolor{1a7862}{2} = a \cdot \textcolor{1a7862}{0} + b$$
$$b = 2$$
Zatem
$$f(x)=ax+2$$
Ponadto
$$f(4)-f(2)=6$$
$$a \cdot 4 + 2 - (a \cdot 2 + 2)=6$$
$$4a + 2 - 2a - 2 = 6$$
$$2a = 6$$
$$a = 3$$